数据结构之AVL树详解(2)
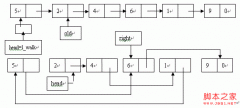
(2) 删除操作:首先定位要删除的节点,然后用该节点的右孩子的最左孩子替换该节点,并重新调整以该节点为根的子树为AVL树,具体调整方法跟插入数据
(2) 删除操作:首先定位要删除的节点,然后用该节点的右孩子的最左孩子替换该节点,并重新调整以该节点为根的子树为AVL树,具体调整方法跟插入数据类似,代码如下:
复制代码 代码如下:
Node_t Delete(Type x, Tree t) {
if(t == NULL) return NULL;
if(t->data == x) {
if(t->right == NULL) {
Node_t temp = t;
t = t->left;
free(temp);
} else {
Node_t head = t->right;
while(head->left) {
head = head->left;
}
t->data = head->data; //just copy data
t->right = Delete(t->data, t->right);
t->height = Max(Height(t->left), Height(t->right)) + 1;
}
return t;
} else if(t->data < x) {
Delete(x, t->right);
if(t->right) Rotate(x, t->right);
} else {
Delete(x, t->left);
if(t->left) Rotate(x, t->left);
}
if(t) Rotate(x, t);
}
5. 总结
AVL树是最早的自平衡二叉树,相比于后来出现的平衡二叉树(红黑树,treap,splay树)而言,它现在应用较少,但研究AVL树对于了解后面出现的常用平衡二叉树具有重要意义。
6. 参考资料
(1) 数据结构(C语言版) 严蔚敏,吴伟民著
(2) http://zh.wikipedia.org/wiki/AVL%E6%A0%91
精彩图集
精彩文章