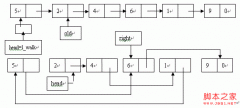
如何用有限个点拟合出光滑的曲线

　　/* 二次抛物线法绘制曲线函数 */

　　void paowuxian(int *x,int *y,int n,unsigned int k)

　　{

　　unsigned int i,j;

　　float t1,t2,t3,t,a,b,c,d,tx,ty;

　　*x=*(x+1);*(y)=*(y+1);

　　*(x+n+1)=*(x+n);*(y+n+1)=*(y+n);

　　t=0.5/k;

　　setcolor(10);

　　moveto(*(x+1),*(y+1));

　　for(i=0;i

　　 {

　　 for(j=1;j

　　 {

　　 t1=j*t;

　　 t2=t1*t1;

　　 t3=t2*t1;

　　 a=4*t2-t1-4*t3;

　　 b=1-10*t2+12*t3;

　　 c=t1+8*t2-12*t3;

　　 d=4*t3-2*t2;

　　 tx=a*(*(x+i))+b*(*(x+i+1))+c*(*(x+i+2))+d*(*(x+i+3));

　　 ty=a*(*(y+i))+b*(*(y+i+1))+c*(*(y+i+2))+d*(*(y+i+3));

　　 lineto(tx,ty);

　　 }

　　 }

　　 lineto(*(x+i+2),*(y+i+2));

　　}

　　/* 二次B样条法绘制曲线函数 */

　　void byangtiao(int *x,int *y,int n,unsigned int k)

　　{

　　unsigned int i,j;

　　float t,t1,t2,a,b,c,tx,ty;

　　*x=*(x+1);*y=*(y+1);

　　*(x+n+1)=*(x+n);*(y+n+1)=*(y+n);

　　t=1.0/k;

　　setcolor(13);

　　moveto((*x+(*(x+1)))/2.0,(*y+(*(y+1)))/2.0);

　　for(i=0;i

　　 {

　　 for(j=1;j

　　 {

　　 t1=j*t;

　　 t2=t1*t1;

　　 a=(t2-2*t1+1)/2.0;

　　 b=t1-t2+1/2.0;

　　 c=t2/2.0;

　　 tx=a*(*(x+i))+b*(*(x+i+1))+c*(*(x+i+2));

　　 ty=a*(*(y+i))+b*(*(y+i+1))+c*(*(y+i+2));

　　 lineto(tx,ty);

　　 }

　　 }

　　}

　　/*这个忘了是什么算法了。：）似乎是叫三次参数样条法*/

　　void parspl(int p[][2],int n,int k)

　　{

　　int i,j;

　　float t1,t2,t3,t,a,b,c,d,x,y;

　　p[0][0]=p[1][0];p[0][1]=p[1][1];

　　p[n+1][0]=p[n][0];p[n+1][1]=p[n][1];

　　t=0.5/k;

　　moveto(p[1][0],p[1][1]+D);

　　for(i=0;i

　　 {

　　 for(j=1;j

　　 {

　　 t1=j*t;

　　 t2=t1*t1;

　　 t3=t2*t1;

　　 a=4*t2-t1-4*t3;

　　 b=1-10*t2+12*t3;

　　 c=t1+8*t2-12*t3;

　　 d=4*t3-2*t2;

　　 x=a*p[i][0]+b*p[i+1][0]+c*p[i+2][0]+d*p[i+3][0];

　　 y=a*p[i][1]+b*p[i+1][1]+c*p[i+2][1]+d*p[i+3][1];

　　 lineto(x,y,15);

　　 }

　　 }

　　 lineto(p[i+2][0],p[i+2][1],15);

　　}