C++数据结构学习:用栈做表达式求值[组图]
栈的应用很广泛，原书只讲解了表达式求值，那我也就只写这些。其实，栈的最大的用途是解决回溯问题，这也包含了消解递归；而当你用栈解决回溯问题成了习惯的时候，你就很少想
栈的应用很广泛，原书只讲解了表达式求值，那我也就只写这些。其实，栈的最大的用途是解决回溯问题，这也包含了消解递归；而当你用栈解决回溯问题成了习惯的时候，你就很少想到用递归了，比如迷宫求解。
![]()
![]()
![]()
![]()
<!-- frame contents -->
<!-- /frame contents -->
![]()
![]()
![]()
![]()
另外，人的习惯也是先入为主的，比如树的遍历，从学的那天开始，就是递归算法，虽然书上也教了用栈实现的方法，但应用的时候，你首先想到的还是递归；当然了，假如语言本身不支持递归（如BASIC），那栈就是唯一的选择了――似乎现在的高级语言都是支持递归的。
如下是表达式类的定义和实现，表达式可以是中缀表示也可以是后缀表示，用头节点数据域里的type区分，这里有一点说明的是，由于单链表的赋值函数，我原来写的时候没有复制头节点的内容，所以，要是在两个表达式之间赋值，头节点里存的信息就丢了。你可以改写单链表的赋值函数来解决这个隐患，或者你根本不不在两个表达式之间赋值也行。
#ifndef EXPression_H
#define Expression_H
#include "List.h"
#include "Stack.h"
#define INFIX 0
#define POSTFIX 1
#define OPND 4
#define OPTR 8
template class ExpNode
{
public:
int type;
union { Type opnd; char optr;};
ExpNode() : type(INFIX), optr('=') {}
ExpNode(Type opnd) : type(OPND), opnd(opnd) {}
ExpNode(char optr) : type(OPTR), optr(optr) {}
};
更多内容请看C/C++技术专题 数据结构 数据结构教程专题，或
template class Expression : List >
{
public:
void Input()
{
MakeEmpty(); Get()->type =INFIX;
cout << endl << "输入表达式，以＝结束输入" << endl;
Type opnd; char optr = ' ';
while (optr != '=')
{
cin >> opnd;
if (opnd != 0)
{
ExpNode newopnd(opnd);
LastInsert(newopnd);
}
cin >> optr;
ExpNode newoptr(optr);
LastInsert(newoptr);
}
}
void Print()
{
First();
cout << endl;
for (ExpNode *p = Next(); p != NULL; p = Next() )
{
switch (p->type)
{
case OPND:
cout << p->opnd; break;
case OPTR:
cout << p->optr; break;
default: break;
}
更多内容请看C/C++技术专题 数据结构 数据结构教程专题，或
cout << ' ';
}
cout << endl;
}
Expression & Postfix() //将中缀表达式转变为后缀表达式
{
First();
if (Get()->type == POSTFIX) return *this;
![]()
![]()
![]()
![]()
<!-- frame contents -->
<!-- /frame contents -->
![]()
![]()
![]()
![]()
Stack s; s.Push('=');
Expression temp;
ExpNode *p = Next();
while (p != NULL)
{
switch (p->type)
{
case OPND:
temp.LastInsert(*p); p = Next(); break;
case OPTR:
while (isp(s.GetTop()) > icp(p->optr) )
{
ExpNode newoptr(s.Pop());
temp.LastInsert(newoptr);
}
if (isp(s.GetTop()) == icp(p->optr) )
{
s.Pop(); p =Next(); break;
}
s.Push(p->optr); p = Next(); break;
default: break;
}
}
*this = temp;
pGetFirst()->data.type = POSTFIX;
return *this;
}
Type Calculate()
{
更多内容请看C/C++技术专题 数据结构 数据结构教程专题，或
Expression temp = *this;
if (pGetFirst()->data.type != POSTFIX) temp.Postfix();
Stack s; Type left, right;
for (ExpNode *p = temp.Next(); p != NULL; p = temp.Next())
{
switch (p->type)
![]()
![]()
![]()
![]()
<!-- frame contents -->
<!-- /frame contents -->
![]()
![]()
![]()
![]()
{
case OPND:
s.Push(p->opnd); break;
case OPTR:
right = s.Pop(); left = s.Pop();
switch (p->optr)
{
case '+': s.Push(left + right); break;
case '-': s.Push(left - right); break;
case '*': s.Push(left * right); break;
case '/': if (right != 0) s.Push(left/right); else return 0; break;
// case '%': if (right != 0) s.Push(left%right); else return 0; break;
// case '^': s.Push(Power(left, right)); break;
default: break;
}
default: break;
}
}
return s.Pop();
}
private:
int isp(char optr)
{
switch (optr)
{
case '=': return 0;
case '(': return 1;
case '^': return 7;
case '*': return 5;
case '/': return 5;
case '%': return 5;
case '+': return 3;
case '-': return 3;
case ')': return 8;
default: return 0;
}
}
int icp(char optr)
更多内容请看C/C++技术专题 数据结构 数据结构教程专题，或
{
switch (optr)
{
case '=': return 0;
case '(': return 8;
case '^': return 6;
case '*': return 4;
case '/': return 4;
case '%': return 4;
![]()
![]()
![]()
![]()
<!-- frame contents -->
<!-- /frame contents -->
![]()
![]()
![]()
![]()
case '+': return 2;
case '-': return 2;
case ')': return 1;
default: return 0;
}
}
};
#endif
更多内容请看C/C++技术专题 数据结构 数据结构教程专题，或
几点说明
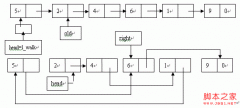
l 表达式用单链表储存，你可以看到这个链表中既有操作数又有操作符，假如你看过我的《如何在一个链表中链入不同类型的对象》，这里的方法也是对那篇文章的补充。
![]()
![]()
![]()
![]()
<!-- frame contents -->
<!-- /frame contents -->
![]()
![]()
![]()
![]()
l 输入表达式时，会将原来的内容清空，并且必须按照中缀表示输入。假如你细看一下中缀表达式，你就会发现，除了括号，表达式的结构是“操作数”、“操作符”、“操作数”、……“操作符（＝）”，为了统一这个规律，同时也为了使输入函数简单一点，规定括号必须这样输入“0（”、“）0”；这样一来，“0”就不能作为操作数出现在表达式中了。因为我没有在输入函数中增加容错的语句，所以一旦输错了，那程序就“死”了。
l 表达式求值的过程是，先变成后缀表示，然后用后缀表示求值。因为原书讲解的是这两个算法，并且用这两个算法就能完成中缀表达式的求值，所以我就没写中缀表达式的直接求值算法。具体算法说明参见原书，我就不废话了。
l Calculate()注释掉的两行，“％”是因为只对整型表达式合法，“^”的Power()函数没有完成。
l isp()，icp()的返回值，原书说的不细，我来多说两句。‘＝’（表达式开始和结束标志）的栈内栈外优先级都是最低。‘（’栈外最高，栈内次最低。‘）’栈外次最低，不进栈。‘^’栈内次最高，栈外比栈内低。‘×÷％’栈内比‘^’栈外低，栈外比栈内低。‘＋－’栈内比‘×’栈外低，栈外比栈内低。这样，综合起来，就有9个优先级，于是就得出了书上的那个表。(CSDN)
更多内容请看C/C++技术专题 数据结构 数据结构教程专题，或
如下是表达式类的定义和实现，表达式可以是中缀表示也可以是后缀表示，用头节点数据域里的type区分，这里有一点说明的是，由于单链表的赋值函数，我原来写的时候没有复制头节点的内容，所以，要是在两个表达式之间赋值，头节点里存的信息就丢了。你可以改写单链表的赋值函数来解决这个隐患，或者你根本不不在两个表达式之间赋值也行。
#ifndef EXPression_H
#define Expression_H
#include "List.h"
#include "Stack.h"
#define INFIX 0
#define POSTFIX 1
#define OPND 4
#define OPTR 8
template class ExpNode
{
public:
int type;
union { Type opnd; char optr;};
ExpNode() : type(INFIX), optr('=') {}
ExpNode(Type opnd) : type(OPND), opnd(opnd) {}
ExpNode(char optr) : type(OPTR), optr(optr) {}
};
更多内容请看C/C++技术专题 数据结构 数据结构教程专题，或
template class Expression : List >{
public:
void Input()
{
MakeEmpty(); Get()->type =INFIX;
cout << endl << "输入表达式，以＝结束输入" << endl;
Type opnd; char optr = ' ';
while (optr != '=')
{
cin >> opnd;
if (opnd != 0)
{
ExpNode newopnd(opnd);
LastInsert(newopnd);
}
cin >> optr;
ExpNode newoptr(optr);
LastInsert(newoptr);
}
}
void Print()
{
First();
cout << endl;
for (ExpNode *p = Next(); p != NULL; p = Next() )
{
switch (p->type)
{
case OPND:
cout << p->opnd; break;
case OPTR:
cout << p->optr; break;
default: break;
}
更多内容请看C/C++技术专题 数据结构 数据结构教程专题，或
cout << ' ';}
cout << endl;
}
Expression & Postfix() //将中缀表达式转变为后缀表达式
{
First();
if (Get()->type == POSTFIX) return *this;
Expression temp;
ExpNode *p = Next();
while (p != NULL)
{
switch (p->type)
{
case OPND:
temp.LastInsert(*p); p = Next(); break;
case OPTR:
while (isp(s.GetTop()) > icp(p->optr) )
{
ExpNode newoptr(s.Pop());
temp.LastInsert(newoptr);
}
if (isp(s.GetTop()) == icp(p->optr) )
{
s.Pop(); p =Next(); break;
}
s.Push(p->optr); p = Next(); break;
default: break;
}
}
*this = temp;
pGetFirst()->data.type = POSTFIX;
return *this;
}
Type Calculate()
{
更多内容请看C/C++技术专题 数据结构 数据结构教程专题，或
Expression temp = *this;if (pGetFirst()->data.type != POSTFIX) temp.Postfix();
Stack s; Type left, right;
for (ExpNode *p = temp.Next(); p != NULL; p = temp.Next())
{
switch (p->type)
case OPND:
s.Push(p->opnd); break;
case OPTR:
right = s.Pop(); left = s.Pop();
switch (p->optr)
{
case '+': s.Push(left + right); break;
case '-': s.Push(left - right); break;
case '*': s.Push(left * right); break;
case '/': if (right != 0) s.Push(left/right); else return 0; break;
// case '%': if (right != 0) s.Push(left%right); else return 0; break;
// case '^': s.Push(Power(left, right)); break;
default: break;
}
default: break;
}
}
return s.Pop();
}
private:
int isp(char optr)
{
switch (optr)
{
case '=': return 0;
case '(': return 1;
case '^': return 7;
case '*': return 5;
case '/': return 5;
case '%': return 5;
case '+': return 3;
case '-': return 3;
case ')': return 8;
default: return 0;
}
}
int icp(char optr)
更多内容请看C/C++技术专题 数据结构 数据结构教程专题，或
{switch (optr)
{
case '=': return 0;
case '(': return 8;
case '^': return 6;
case '*': return 4;
case '/': return 4;
case '%': return 4;
case '-': return 2;
case ')': return 1;
default: return 0;
}
}
};
#endif
更多内容请看C/C++技术专题 数据结构 数据结构教程专题，或
几点说明l 表达式用单链表储存，你可以看到这个链表中既有操作数又有操作符，假如你看过我的《如何在一个链表中链入不同类型的对象》，这里的方法也是对那篇文章的补充。
l 表达式求值的过程是，先变成后缀表示，然后用后缀表示求值。因为原书讲解的是这两个算法，并且用这两个算法就能完成中缀表达式的求值，所以我就没写中缀表达式的直接求值算法。具体算法说明参见原书，我就不废话了。
l Calculate()注释掉的两行，“％”是因为只对整型表达式合法，“^”的Power()函数没有完成。
l isp()，icp()的返回值，原书说的不细，我来多说两句。‘＝’（表达式开始和结束标志）的栈内栈外优先级都是最低。‘（’栈外最高，栈内次最低。‘）’栈外次最低，不进栈。‘^’栈内次最高，栈外比栈内低。‘×÷％’栈内比‘^’栈外低，栈外比栈内低。‘＋－’栈内比‘×’栈外低，栈外比栈内低。这样，综合起来，就有9个优先级，于是就得出了书上的那个表。(CSDN)
更多内容请看C/C++技术专题 数据结构 数据结构教程专题，或精彩图集
精彩文章