教学计划编制问题

问题描述；

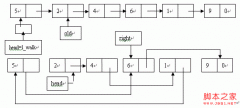
大学的每个专业都要编制教学计划。假设任何专业都有固定的学习年限，每学年含两学期，每学期的时间长度和学分上限都相等。每个专业开设的课程都是确定的，而且课程的开设时间的安排必须满足先修关系。每个课程的先修关系都是确定的，可以有任意多门，也可以没有。每一门课程恰好一个学期。试在这样的情况下设置一个教学计划编制程序。

基本要求：

（1）：输入参数：学期总数，一学期的学分上限，每门课的课程号，学分，直接先修关系的课程号。

（2）：课程号尽可能的集中在前几个学期中。

（3）：若无解，则报告错误信息；否则见教学计划输入到指定的文件中。计划的表格格式自行设计。

以下为我设计的一段程序，其中有一些错误，并且将教学计划输入到指定的文件中这一要求没有完成，望一并指正和修改，因为该问题为我的课程设计，十分的急迫，我将表示无限的感激并永远的支持该网站！

/* 输出有向图的一个拓扑序列及其应用问题的算法实现程序 */

　　 #include

　　 #include

　　 #include // malloc()等

　　 #include // INT_MAX等

　　 #include // EOF(=^Z或F6),NULL

　　 #include // atoi()52

　　 #include // eof()

　　 #include // floor(),ceil(),abs()

　　 #include // exit()

　　 #include // cout,cin

　　 // 函数结果状态代码

　　 #define TRUE 1

　　 #define FALSE 0

　　 #define OK 1

　　 #define ERROR 0

　　 #define INFEASIBLE -1

　　 typedef int Status; // Status是函数的类型,其值是函数结果状态代码，如OK等

　　 typedef int Boolean; // Boolean是布尔类型,其值是TRUE或FALSE

　　 #define MAX_NAME 10

　　 /* 顶点字符串的最大长度 */

　　 #define MAXCLASS 100

　　 int Z=0;

　　 int X=0;

　　 int xqzs,q=1,xfsx;

　　 typedef int InfoType;

　　 typedef char VertexType[MAX_NAME]; /* 字符串类型 */

　　 /* 图的邻接表存储表示 */

　　 #define MAX_VERTEX_NUM 100

　　 typedef enum{DG}GraphKind; /* {有向图,有向网,无向图,无向网} */

　　 typedef strUCt ArcNode

　　 {

　　 int adjvex; /* 该弧所指向的顶点的位置 */

　　 struct ArcNode *nextarc; /* 指向下一条弧的指针 */

　　 InfoType *info; /* 网的权值指针） */

　　 }ArcNode; /* 表结点 */

　　 typedef struct

　　 {

　　 VertexType data; /* 顶点信息 */

　　 ArcNode *firstarc; /* 第一个表结点的地址,指向第一条依附该顶点的弧的指针 */

　　 }VNode,AdjList[MAX_VERTEX_NUM]; /* 头结点 */

　　 typedef struct

　　 {

　　 AdjList vertices,verticestwo;

　　 int vexnum,arcnum; /* 图的当前顶点数和弧数 */

　　 int kind; /* 图的种类标志 */

　　 }ALGraph;

　　/* 图的邻接表存储的基本操作 */

　　 int LocateVex(ALGraph G,VertexType u)

　　{ /* 初始条件: 图G存在,u和G中顶点有相同特征 */

　　 /* 操作结果: 若G中存在顶点u,则返回该顶点在图中位置;否则返回-1 */

　　 int i;

　　 for(i=0;i

　　 if(strcmp(u,G.vertices[i].data)==0)

　　 return i;

　　 return -1;

　　}

　　Status CreateGraph(ALGraph *G)

　　 { /* 采用邻接表存储结构,构造没有相关信息的图G(用一个函数构造4种图) */

　　 int i,j,k;

　　 VertexType va,vb;

　　 ArcNode *p;

　　 printf("请输入教学计划的课程数: ");

　　 scanf("%d",&(*G).vexnum);

　　 printf("请输入拓扑排序所形成的课程先修关系的边数: ");

　　 scanf("%d",&(*G).arcnum);

　　 printf("请输入%d个课程的代表值(<%d个字符):

",(*G).vexnum,MAX_NAME);

　　 for(i=0;i<(*G).vexnum;++i) /* 构造顶点向量 */

　　 { scanf("%s",(*G).vertices[i].data);

　　 (*G).vertices[i].firstarc=NULL;

　　 }

　　 printf("请输入%d个课程的学分值(<%d个字符):

",(*G).vexnum,MAX_NAME);

　　 for(i=0;i<(*G).vexnum;++i) /* 构造顶点向量 */

　　 {scanf("%s",(*G).verticestwo[i].data);

　　 }

　　 printf("请顺序输入每条弧(边)的弧尾和弧头(以空格作为间隔):

");

　　 for(k=0;k<(*G).arcnum;++k) /* 构造表结点链表 */

　　 { scanf("%s%s",va,vb);

　　 i=LocateVex(*G,va); /* 弧尾 */

　　 j=LocateVex(*G,vb); /* 弧头 */

　　 p=(ArcNode*)malloc(sizeof(ArcNode));

　　 p->adjvex=j;

　　 p->info=NULL; /* 图 */

　　 p->nextarc=(*G).vertices[i].firstarc; /* 插在表头 */

　　 (*G).vertices[i].firstarc=p;

　　 }

　　 return OK;

　　 }

　　void Display(ALGraph G)

　　 { /* 输出图的邻接矩阵G */

　　 int i;

　　 ArcNode *p;

　　 switch(G.kind)

　　 {case DG: printf("有向图

");

　　 }

　　 printf("%d个顶点：

",G.vexnum);

　　 for(i=0;i

　　 printf("%s ",G.vertices[i].data);

　　 printf("

%d条弧(边):

",G.arcnum);

　　 for(i=0;i

　　 {

　　 p=G.vertices[i].firstarc;

　　 while(p)

　　 {printf("%s→%s ",G.vertices[i].data,G.vertices[p->adjvex].data);

　　 p=p->nextarc;

　　 }

　　 printf("

");

　　 }

　　 }

　　void FindInDegree(ALGraph G,int indegree[])

　　 { /* 求顶点的入度，算法调用 */

　　 int i;

　　 ArcNode *p;

　　 for(i=0;i

　　 indegree[i]=0; /* 赋初值 */

　　 for(i=0;i

　　 {

　　 p=G.vertices[i].firstarc;

　　 while(p)

　　 { indegree[p->adjvex]++;

　　 p=p->nextarc;

　　 }

　　 }

　　 }

　　 typedef int SElemType; /* 栈类型 */

　　 /*栈的顺序存储表示 */

　　 #define STACK_IN99v_SIZE 10 /* 存储空间初始分配量 */

　　 #define STACKINCREMENT 2 /* 存储空间分配增量 */

　　 typedef struct SqStack

　　 {

　　 SElemType *base; /* 在栈构造之前和销毁之后，base的值为NULL */

　　 SElemType *top; /* 栈顶指针 */

　　 int stacksize; /* 当前已分配的存储空间，以元素为单位 */

　　 }SqStack; /* 顺序栈 */

　　 /* 顺序栈的基本操作 */

　　 Status InitStack(SqStack *S)

　　 { /* 构造一个空栈S */

　　 (*S).base=(SElemType *)malloc(STACK_IN99v_SIZE*sizeof(SElemType));

　　 if(!(*S).base)

　　 exit(OVERFLOW); /* 存储分配失败 */

　　 (*S).top=(*S).base;

　　 (*S).stacksize=STACK_IN99v_SIZE;

　　 return OK;

　　}

　　Status StackEmpty(SqStack S)

　　 { /* 若栈S为空栈，则返回TRUE，否则返回FALSE */

　　 if(S.top==S.base)

　　 return TRUE;

　　 else

　　 return FALSE;

　　}

　　 Status Pop(SqStack *S,SElemType *e)

　　 { /* 若栈不空，则删除S的栈顶元素，用e返回其值，并返回OK；否则返回ERROR */

　　 if((*S).top==(*S).base)

　　 return ERROR;

　　 *e=*--(*S).top;

　　 return OK;

　　 }

　　 Status Push(SqStack *S,SElemType e)

　　 { /* 插入元素e为新的栈顶元素 */

　　 if((*S).top-(*S).base>=(*S).stacksize) /* 栈满，追加存储空间 */

　　 {

　　 (*S).base=(SElemType *)realloc((*S).base,((*S).stacksize+STACKINCREMENT)*sizeof

[1] [2]