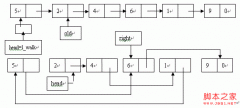
基于C++的稀疏矩阵乘法运算器的实现(2)

For ( scanf( & i, & j, & e); i!=0 ; scanf ( &I, & j, &e ) ){

　　　 If(! ( p=(OLNode * )malloc( sizeof (OLNode) ) ) ) exit ( OVERFLOW )

　　　 P―>i = i;　　 p―>j=j ;　　 p―>e=e;

　　　 If (M . rhead [ i ] = =NULL)　 M . rhead [ i ] = p;

　　　 Else{

For ( q = M . rhead [ i ]; ( q―>right ) && q―> right―> j < j;　 q = q―> right;)

p―>right =q―>right ;　 q―>right=p;　 }

if (M . chead [ j ] = =NULL)　　 M . chead[ j ]=p;

else{

　　 For ( q=M . chead [ j ] ; (q―>down) && q―>down―> i < i ; q = q―>down;)

　　　　　　　　　　　　　 p―>down = q―>down;

q―>down = p ;}

　　　　　　　　　　 }

　　　　　　　 Return OK;

}//CreateSMatrix_OL

　　2.2.2 疏矩阵的相乘运算

Status MultSMatrix(RLSMatrix M, RLSMatrix N ,RLSMatrix & Q){

　　　 //求矩阵乘积Q=M*N

　　　 if(M . nu! = N . mu)　 return　 ERROR;

　　　 Q . mu=M . mu;　 Q . nu = N . nu ; Q . tu= 0;

　　　 If (M . tu* N . tu ! = 0) {

　　　　　　　 For　 ( arow=1 ; arrow<=M.mu; ++arrow ){

　　　　　　　　　　　 Ctemp[　 ]= 0;

　　　　　　　　　　　 Q.rpos[arrow]=Q . tu + 1;

　　　　　　　　　　　 For ( p = M . rpos[arrow]; p

　　　　　　　　　　　　　　　　 brow = M .data [ p ] . j;

　　　　　　　　　　　　　　　　 if ( brow

　　　　　　　　　　　　　　　　 else {t=N.tu+1}

　　　　　　　　　　　　　　　　 for ( q = N . rpoe[ brow ];　 q

　　　　　　　　　　　　　　　　　　　 ccol = N . data[q] . j;

　　　　　　　　　　　　　　　　　　　 ctemp[ ccol ] += M . data[ p ] . e * N . data[ q ] . e;