基于C++的稀疏矩阵乘法运算器的实现(3)

　　　　　　　　　　　　　　　　 }//for q

　　　　　　　　　　　 }

　　　　　　　　　　　 for ( ccol = 1 ; ccol <= Q.nu;　 ++ccol )

　　　　　　　　　　　　　　　　 if (ctemp[ccol]){

　　　　　　　　　　　　　　　　　　　 if (++Q . tu > MAXSIZE)　 return ERROR;

　　　　　　　　　　　　　　　　　　　 Q.data[ Q . tu ] = { arrow, ccol, ctemp[ccol] };

}

}

　　　　　　　　　 }

　　　　　　　 return OK;

}

　　3 实验及其调试

　　3.1 测试数据

4　 -3　 0　　 0　　 1　　　　　　　　　　　　　　　 3　 0　 0　　　　　　 0　　 -6　　　 0

0　　 0　 0　　 8　　 0　　　　　　 ×　　　　　　 4　 2　 0　　　　　　 8　　 0　　　 0

0　　 0　 1　　 0　　 0　　　　　　　　　　　　　　　 0　 1　 0　　　 =　 0　　　 1　　　 0

0　　 0　 0　　 0　　 70　　　　　　　　　　　　　　 1　 0　 0　　　　　　 0　　　 0　　　 0

　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　0　 0　 0

　　3.2 调试报告

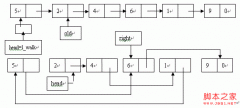
　　 稀疏矩阵相乘的基本操作是：对于M中每个元素M . data . j = N . data [ q ] . i 的元素

　　N . data[ q ],求得M . data[ p ] . v和N . data[ q ] . v的乘积，而乘积矩阵Q中每个元素的值是个累计和，这个乘积M . data[ p ] . v * n . data[ q ]只是Q( i , j )中的一部分。为便于操作，应对每个元素设一累计和的变量，起初值为零，然后扫描数组M，求得相应元素的乘积并累加到适当的求累计的变量上

　　 累加器ctemp的初始的时间复杂度为O（M . mu * N . nu ）,求Q的所有非零元的时间复杂度为O（M . tu * N . tu / N . mu）,进行压缩存储的时间复杂度为O（M . mu * N . nu）,因此，总的时间复杂度为O（M.mu * N.nu+M.tu * N.tu / N.mu）。

　　 在调试过程中，在程序的建立十字链表时的插入过程中，对插入元素的列和整个矩阵的列时常混淆造成出错，以及在建立十字链表的行列头链表时，并没考虑行列的大小问题，即没有考虑m, n的大小。

　　4 结束语

　　 本文采用标准C++语言实现了稀疏矩阵乘法运算器的实现, 通过一个实例验证了所实现算法的正确性, 培养了对编程的兴趣，同时也提高了编程的能力. 同时, 本文中所设计的关于稀疏矩阵数据的存储, 稀疏矩阵的创建以及稀疏矩阵相乘对初学者具有一定的指导作用.