经典四讲贯通C++排序之四 选择排序(1)(2)

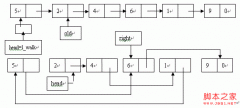
锦标排序

从直选排序看来，算法的瓶颈在于KCN，而实际上，对于后续的寻找最小值来说，时间复杂度可以降到O(logn)。最为直接的做法是采用锦标赛的办法，将冠军拿走之后，只要把冠军打过的比赛重赛一遍，那么剩下的人中的“冠军”就产生了，而重赛的次数就是竞赛树的深度。实际写的时候，弄不好就会写得很“蠢”，不只多余占用了大量内存，还会导致无用的判断。我没见过让人满意的例程(殷版上的实在太恶心了)，自己又写不出来漂亮的，也就不献丑了(其实这是惰性的缘故，有了快排之后，大多数人都不会对其他内排感兴趣，除了基数排序)。实在无聊的时候，不妨写(或者改进)锦标排序来打发时间，^_^。

堆排序

锦标排序的附加储存太多了，而高效的寻找最大值或最小值(O(logn))，我们还有一种方法是堆。这里使用了最大堆，用待排记录的空间充当堆空间，将堆顶的记录(目前最大)和堆的最后一个记录交换，当堆逐渐缩小成1的时候，记录就排序完成了。显而易见的，时间复杂度为O(nlogn)，并且没有很糟的情况。

template <class T>  
void FilterDown(T a[], int i, int N, int& KCN, int& RMN)  
{  
int child = 2 * i + 1; T temp = a[i];  
while (child < N)  
{  
if (child < N - 1 && a[child] < a[child+1]) child++;  
if (++KCN && temp >= a[child]) break;//不需调整，结束调整  
a[i] = a[child]; RMN++;  
i = child; child = 2 * i + 1;  
}  
a[i] = temp; RMN++;  
}  
template <class T>  
void HeapSort(T a[], int N, int& KCN, int& RMN)  
{  
int i;  
for (i = (N - 2)/2; i >= 0; i--) FilterDown(a, i, N, KCN, RMN);//生成最大堆  
for (i = N - 1; i > 0; i--)  
{  
swap(a[0], a[i]); RMN += 3;  
FilterDown(a, 0, i, KCN, RMN);  
}  
} 

测试结果，直接测试的是N=100000：

Sort ascending N=100000 TimeSpared: 110ms  
KCN=1556441 KCN/N=15.5644 KCN/N^2=0.000155644KCN/NlogN=0.937071  
RMN=2000851 RMN/N=20.0085 RMN/N^2=0.000200085RMN/NlogN=1.20463  
Sort randomness N=100000 TimeSpared: 160ms  
KCN=3047006 KCN/N=30.4701 KCN/N^2=0.000304701KCN/NlogN=1.83448  
RMN=3898565 RMN/N=38.9857 RMN/N^2=0.000389857RMN/NlogN=2.34717  
Sort descending N=100000 TimeSpared: 90ms  
KCN=4510383 KCN/N=45.1038 KCN/N^2=0.000451038KCN/NlogN=2.71552  
RMN=5745996 RMN/N=57.46 RMN/N^2=0.0005746 RMN/NlogN=3.45943 

整体性能非常不错，附加储存1，还没有很糟的情况，如果实在不放心快排的最坏情况，堆排确实是个好选择。这里仍然出现了KCN、RMN多的反而消耗时间少的例子――误差70ms是不可能的，看来CPU优化的作用还是非常明显的(可能还和Cache有关)。